参考:
- https://zhuanlan.zhihu.com/p/267884783
- https://www.cnblogs.com/idreamo/p/9411265.html
- https://blog.csdn.net/qq_39972971/article/details/82346390
- https://www.cnblogs.com/RioTian/p/13928916.html
- https://www.cnblogs.com/book-book/p/6349362.html
- https://oi-wiki.org/math/number-theory/pollard-rho/
- https://zhuanlan.zhihu.com/p/220203643
分解质因数
引入
给定一个正整数 ,试快速找到它的一个 非平凡因数 ( 除了1和数本身以外的因数 )。
朴素算法
考虑朴素算法——试除法,因数是成对分布的, 的所有因数可以被分成两块,即 和 。只需要把 ) 里的数遍历一遍,再根据除法就可以找出至少两个因数了。这个方法的时间复杂度为 。
最简单的算法即从 进行遍历。
vector<int> breakdown(int N) { vector<int> result; for (int i = 2; i * i <= N; i++) { if (N % i == 0) { // 如果 i 能够整除 N,说明 i 为 N 的一个质因子。 while (N % i == 0) N /= i; result.push_back(i); } } if (N != 1) { // 说明再经过操作之后 N 留下了一个素数 result.push_back(N); } return result;}我们能够证明 result 中的所有元素均为 N 的素因数。
首先证明元素均为 的素因数:因为当且仅当 N % i == 0 满足时,result 发生变化: 储存 ,说明此时 能整除 ,说明了存在一个数 使得 ,即 (其中, 为 自身发生变化后遇到 时所除的数。我们注意到 result 若在 之前就已经有数了,为 ,那么有 ,被除的乘积即为 )。所以 i 为 N 的因子。
其次证明 result 中均为素数。我们假设存在一个在 result 中的合数 ,并根据算术基本定理,分解为一个素数序列 ,而因为 ,所以它一定会在 之前被遍历到,并令
while(N % k1 == 0) N /= k1,即让N没有了素因子 ,故遍历到 时,N 和 K 已经没有了整除关系了。
值得指出的是,如果开始已经打了一个素数表的话,时间复杂度将从 下降到 。具体可以去了解 筛法 的相关知识。【埃筛 欧筛】
但是,当 是个大整数时( ),这个算法的运行时间是不优秀的。我们期望一个更优秀的算法。
这里给出一种想法,即:通过随机的方法,猜测一个数是不是 的因数,如果运气好可以在 的时间复杂度下求解答案,但是对于的数据 是个大整数时( ),成功猜测的概率是 , , 期望猜测的次数是 。如果是在) 里进行猜测,成功率会大一些。
template <class T>T randint(T l, T r = 0) // 生成随机数建议用<random>里的引擎和分布,而不是rand()模数,那样保证是均匀分布{ static mt19937 eng(time(0)); if (l > r) swap(l, r); uniform_int_distribution<T> dis(l, r); return dis(eng);}int find_factor(int n){ if (is_prime(n)) // 特判素数 return n; int x, d; do { x = randint(2, n - 1); // 生成2和n-1之间的随机数 d = gcd(n, x); // 求gcd } while (d == 1); return d;}在最差的情况下, (p是质数),这时 里只有 1 个 p 是 n 的因数;然而,当 取 时,都有 ,而公因数自然是 n 的因数 。所以此时最差期望时间复杂度可以降到 (gcd的复杂度log,根号来自 有约 种满足条件的选择) ,当然,它连朴素的试除法都比不过。
因此,我们仍希望有方法来优化猜测。
Pollard Rho 算法
生日悖论
为了尝试优化,我们或许需要了解生日悖论。
生日悖论不算严格意义上的悖论,只是反直觉罢了。
这里给出一个简易的表述:一个房间里有23个人,则他们中有两人生日相同的概率超过一半(不考虑闰年)。关于证明:即 。
为了破除旧的生日悖论的直觉,建立新的认识,我们尝试去解决生日悖论的提问:一个房间中至少多少人,才能使其中两个人生日相同的概率达到 ?
解:假设一年有 n 天,房间中有 k 人,用整数 1,2,…,k 对这些人进行编码。假定每个人的生日均匀分布于 n 天之中,且两个人的生日相互独立。 设 k 个人生日互不相同为事件 A,则事件 A 的概率为: , 至少有两个人生日相同的概率为 。 根据题意得,那么有 由不等式 可得:
因此, 将 带入得:。所以一个房间中至少23人,使其中两个人生日相同的概率达到 。而当 时,出现两个人同一天生日的概率将大于一 。 那么在一年有 天的情况下,当房间中有 个人时,至少有两个人的生日相同的概率约为 。
这时,我们可以建立这样一个直觉:如果我们不断在某个范围内生成随机整数,很快便会生成到重复的数,期望大约在根号级别。精确地说,对于一个 内整数的理想随机数生成器,生成序列中第一个重复数字前期望有 个数。 证明参见知乎问答
这里我们回归到原题,对于最坏的情形 ,如果我们不断在 间生成随机数,那么期望在生成大约 个数后,可以出现 个在模 下相同的数(注意 间的随机数模 大致是 间的随机数)。那么这 个数的差的绝对值 ,就一定满足 ,也就满足 。
但是知晓这件事的意义并不是那么大。正如生日悖论虽然正确,但你不一定等在班上遇到和自己生日相同的人,因为这个高概率是在两两比较下才成立的。对于这 个数两两验证,复杂度还是立刻回到 ,这并没有什么进步,所以我们需要一些技巧。
利用最大公约数求出一个因数 || 伪随机数序列
我们再次回顾一下这个性质: 和 某个数 的最大公约数一定是 的因数,即 ,只要选择恰当的 使得 ,就可以求得 的一个约数 。满足这样条件的 不少, 有若干个质因子,每个质因子及其大部分倍数都是可行的。
我们通过 来生成一个序列 :随机取一个 ,令 。其中 是一个随机选取的常数。
举个例子,取 , 生成数据为:
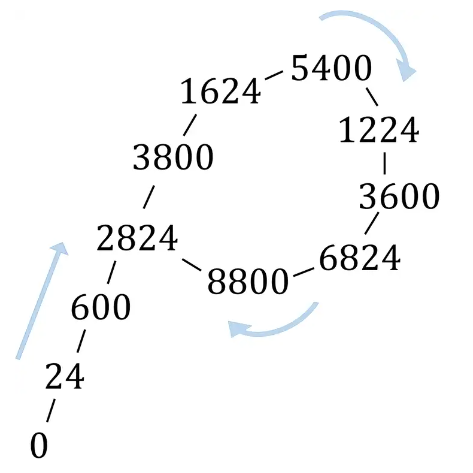
可以发现数据在 以后都在 之间循环。如果将这些数如上图一样排列起来,会发现这个图像酷似一个𝜌,算法也因此得名 。 不难发现这是显然的,因为每个数都是由前一个数决定的,可生成的数又是有限的,那么迟早会进入循环。当然,这个循环极大可能是混循环。
而之所以选择 这个函数生成序列,是因为它有一个性质:
